Types Of Engineering Stresses
Stress
When we applied external load in the body, the deformation produces in the body. The body tries to resist the deformation that resistance per unit area that is stress.
Consider we have a body. There is an applied load on the body at two ends of the body as shown in the figure. The body starts to resist that load in the opposite direction.
P = External load
∑FR= Resistance force
σ(Stress) = ∑FR /A
A = Area
The body is static equilibrium.
So ∑FR =P
σ(Stress) = P /A
The unit of the stress is "N/mm2" or "N/m2" or "Pa".
1. Tensile Stress
2. Compressive Stress
3. Shear Stress
4. Torsional Shear Stress
5. Crushing Stress
6. Bearing Stress
7. Bending Stress
1. Tensile Stress
When the load is passing through axis then the load will try to pull the rod and pulling action call tensile load and stress developed in the material is called tensile stress.
The value of the load is the same but the the the direction is opposite in the shaft. L is the length of the shaft and d is the diameter of the shaft.
Because of the pull-type of load in the shaft, the stress developed in the shaft is called stress.
2. Compressive Stress
It is stress produced in the member due to push load is called compressive stress.
In this shaft push type of load applied at the end of the shaft. because of the the the push type of loading stress developed in the shaft that stress is called compressive stress.
Here area A = πd2/4
3. Shear Stress
Suppose upper plate force acting toward right and bottom plate force acting toward left. Because of two forces which are acting the top and bottom plate can sliding in their direction because of that rivet can break at the junction.
Now it is very much clear from the diagram that because of the action of these two opposite forces rivet break in two parts and that action called shearing action. The load is tension to the area of river diameter. So area A = πd2/4.
In the case of shear Stress, the load is tangential to the cross-section rea.
Shearing may be single shear or double shear.
We have three plates and load which is acting for the top and bottom plate toward the right and middle plate toward the left. Because of acting opposite forces, there is a chance to rivet breaking at two junctions and we are getting three-part their this is the use of double shear Stress.
4. Torsional Shear Stress
Because of torsion, it is related to a rotating motion.
Suppose a rod which is rotating motion and have a bearing which at one end shaft but then the haft is continuously rotating. But bearing is a stationary parameter which tries to stop down the rotating motion of the shaft. This bearing is tried to rotate that part in the opposite direction. Somehow that shaft rotating clockwise direction so twisting happened in the shaft. That twisting is torsion effects. That produces the stress in the shaft and that called torsion stress.
5. Crushing Stress.
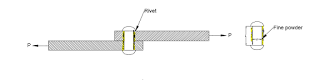
When the load is applied rivet is not break. It can just crush.
It is localized stress acting on a member irrespective type of loading.
Crushing is also called as local compression. Because of crushing its material can not break but it will be a crush into a fine powder.
It can not be a break but its surface will be converted into a fine powder.
The area which is undergoing crush is the projected area.
Area A = πdL.
6. Bearing Stress
It is similar to crushing Stress but the difference is in members are stationary like a pin, cutter, bolts, Nuts they are members of crush.
But in case of bearing the members should rotate and they are circular cross-section.
When the shaft is rotating. there is torque will provide. There are chances of that bush to get warn out because the material of the bush is mostly soft. For example, it can rubber, brass, gunmetal, bronze, etc. And shaft mostly steel which is harder compare to the bush so there is a chance to bush get worn out because of continuous rotation of the shaft. And the failure which is there. It is called as bearing failure. The stress which is developed in the bush that is called as bearing stress.
Bearing stress is most frequently seen in those members which are continually rotating.
A shaft rotating in bush bearing area A = πdl
d = shaft diameter,
l = bush length.
Bearing stress = bearing load/Bearing area.
7. Bending Stress
We have a beam which is simply supported at two ends that is called A and B. Length of the beam is L. Because of the action of central load which is W, the beam it can bend.
Similarly I have a cantilever beam, if the load is acting, beam will be deflected downward. Because of bending, stress which is developed in to the beam that is called as bending stress.
It is the stress developed in a member because of bending load.
Bending stress(σb)
It is denoted by σb.
It can calculated by using flexural formula :
M/I = σb/Y
M = bending moment,
I = moment of inertia
Y = distance at maximum bending occur
0 Comments